Create a Mirror Binary Tree

Problem Description

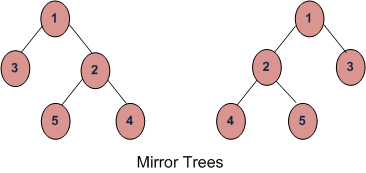
Given a binary tree, return the root of the mirror binary tree. Mirror binary tree of a binary tree is a binary tree with left and right children of all nodes interchanged.


Input format
First line contains an integer t - Number of test cases.
First line of each test case contains an integer n - Number of nodes.
Second line of each test case contains n integers - Value of nodes.
Next n lines contain 3 space separated integers i, l, r describing left and right child of ith node as l and r respectively.

Output format
Print the inorder traversal of the mirror tree in a separate line for each test case.

Sample Input 1
2
4
10 5 9 7
1 2 3
2 -1 -1
3 4 -1
4 -1 -1
3
4 9 3
1 2 3
2 -1 -1
3 -1 -1

Sample Output 1
9 7 10 5
3 4 9

Solution:
To solve the problem of creating a mirror image of a binary tree and printing its in-order traversal, we can follow these steps:
1. **Construct the Binary Tree**: Parse the input to construct the binary tree.
2. **Mirror the Binary Tree**: Recursively swap the left and right children of every node in the tree.
3. **Perform In-order Traversal**: Perform an in-order traversal on the mirrored tree and collect the results.
4. **Print the Results**: Print the in-order traversal for each test case.

Here's how we can implement this in C++:
### C++ Implementation

#include <iostream>
#include <vector>
using namespace std;

class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class BinaryTree {
public:
TreeNode* createTree(const vector<int>& values, const vector<pair<int, int>>& children, int index) {
if (index == -1) return nullptr;
TreeNode* node = new TreeNode(values[index - 1]);
node->left = createTree(values, children, children[index - 1].first);
node->right = createTree(values, children, children[index - 1].second);
return node;
}

TreeNode* mirrorTree(TreeNode* root) {
if (root == nullptr) return nullptr;
TreeNode* left = mirrorTree(root->left);
TreeNode* right = mirrorTree(root->right);
root->left = right;
root->right = left;
return root;
}

void inorderTraversal(TreeNode* root, vector<int>& result) {
if (root == nullptr) return;
inorderTraversal(root->left, result);
result.push_back(root->val);
inorderTraversal(root->right, result);
}
};

int main() {
int t;
cin >> t;

while (t--) {
int n;
cin >> n;
vector<int> values(n);
for (int i = 0; i < n; ++i) {
cin >> values[i];
}

vector<pair<int, int>> children(n);
for (int i = 0; i < n; ++i) {
int node, left, right;
cin >> node >> left >> right;
children[node - 1] = {left, right};
}

BinaryTree bt;
TreeNode* root = bt.createTree(values, children, 1);
root = bt.mirrorTree(root);

vector<int> result;
bt.inorderTraversal(root, result);

for (int val : result) {
cout << val << " ";
}
cout << endl;
}

return 0;
}

### Explanation
1. **TreeNode Class**: Represents each node in the binary tree with a value and pointers to left and right children.
2. **BinaryTree Class**:
- **createTree Function**: Constructs the binary tree from the input values and child indices.
- **mirrorTree Function**: Recursively swaps the left and right children of each node to create the mirror image of the tree.
- **inorderTraversal Function**: Performs an in-order traversal of the tree and stores the result in a vector.
3. **main Function**:
- Reads the number of test cases.
- For each test case, reads the input values and constructs the binary tree using the `createTree` function.
- Mirrors the tree using the `mirrorTree` function.
- Computes the in-order traversal of the mirrored tree using the `inorderTraversal` function.
- Prints the in-order traversal for each test case.

### Input and Output

- **Input**:
- The first line contains the number of test cases `t`.
- For each test case:
- The first line contains the number of nodes `n`.
- The second line contains `n` space-separated integers representing the values of the nodes.
- The next `n` lines contain three integers each, representing the node index and its left and right children.

- **Output**:
- A space-separated list of values representing the in-order traversal of the mirror image of the tree for each test case.

### Sample Input and Output

- **Sample Input**:
```
2
4
10 5 9 7
1 2 3
2 -1 -1
3 4 -1
4 -1 -1
3
4 9 3
1 2 3
2 -1 -1
3 -1 -1
```
- **Sample Output**:
```
9 7 10 5
3 4 9
```

This implementation ensures that we accurately create the mirror image of the binary tree and perform the in-order traversal to generate the desired output.