Find the Largest Forward Diagonal in C++

Problem Description

Given a matrix M, you need to find the forward diagonal having maximum sum. Forward diagonal starts in the left most column or the top most row and ends at the bottom most row or the right most column.

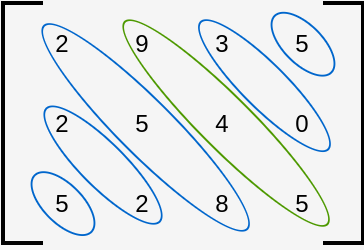
In the following figure there are 6 forward diagonals and the green diagonal is having the maximum sum.

Input Format

First line contains two space-separated integers n,m - The number of rows & columns in the matrix M

Each of the next n lines contains m space-separated integers - The matrix M

Output Format

Print the sum of elements of the largest forward diagonal.

Constraints

1 <= n,m <= 10^3

M[i][j] <= 10^6

Sample Input 1

3 4

2 9 3 5

2 5 4 0

5 2 8 5

Sample Output 1

18

 #include <bits/stdc++.h>

using namespace std;

int largestForwardDiagonal(const vector<vector<int>> &A){

    int result = 0;

    int M = A.size();

    int N = A[0].size();

    for (int j = 0; j < N; j++) {

        int row=0, col=j;

        // Diagonal sums

        int tempsum = 0;

        while (row < M && col < N) {

            tempsum += A[row][col];

            row++;

            col++;

        }

 

        // Update maxSum with

        // the maximum sum

        result = max( tempsum, result );

    }

//for (int i = 0; i < M; i++) {

//We can use i=0 as well instead of i=1 as we have used below.

    for (int i = 1; i < M; i++) {

        int row=i, col=0;

        // Diagonal sums

        int tempsum = 0;

        while (row < M && col < N) {

            tempsum += A[row][col];

            row++;

            col++;

        }

 

        // Update maxSum with

        // the maximum sum

        result = max( tempsum, result );

    }

    return result;

}

int main(){

    int n, m;

    cin>>n>>m;

    vector<vector<int>>M(n,vector<int>(m));

    for (int i = 0; i < n; i++)

    {

        for (int j = 0; j < m; j++)

        {

            cin>>M[i][j];

        }

    }

    int result = largestForwardDiagonal(M);

    cout<<result;

}